Je kunt ook het eerste gedeelte van dit twee minuten durende filmpje bekijken.
Koch-kromme
Elke fractal begint met een lijnstuk met lengte 1 (stap 0) en in stap 1 wordt vastgelegd hoe dat lijnstuk veranderd wordt. In het geval van de Koch-kromme wordt het lijnstuk in drie gelijke stukken verdeeld en het middelste stuk wordt er twee keer tussen geplaatst, zodat er een gelijkzijdige driehoek ontstaat.
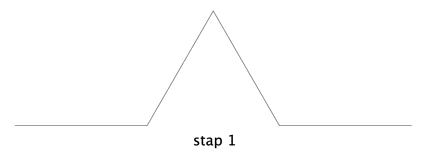
Vervolgens wordt in de stap 2 elke lijnstuk weer op dezelfde manier veranderd. Bij elke volgende stap gebeurt steeds hetzelfde.
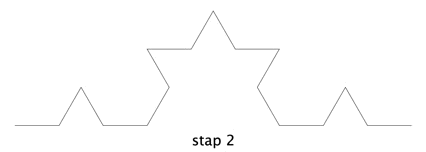
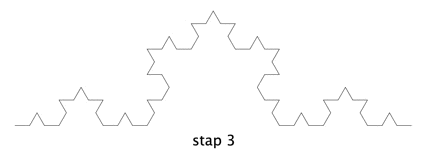
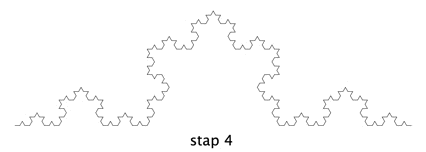
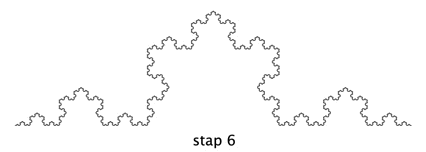
In stap 7 zijn de lijnstukjes al niet meer te onderscheiden en er lijkt een vloeiende kromme te ontstaan. Als je zou inzoomen, zie je de lijnstukjes weer.
Echt vloeiend wordt de kromme pas als je dit proces oneindig zou voortzetten. Dat kan natuurlijk niet, maar een wiskundige denkt daar toch over na. Voor een wiskundige heeft een lijn(stuk) ook geen dikte, maar wij tekenen toch een beetje dikte, anders valt er niets te zien…
Eigenschappen
Lengte
In stap 1 is de totale lengte van de lijn vier keer eenderde =
geworden. Bij elke volgende stap wordt elk lijnstukje weer met 
vermenigvuldigd en daarmee dus ook de totale lengte. De lijn groeit exponentieel en wordt uiteindelijk oneindig lang.Oppervlakte
De oppervlakte onder de lijn blijft beperkt. Hieronder is de oppervlakte getekend bij stap 7. Uiteindelijk wordt de oppervlakte ongeveer 0,866.
Dimensie
Met de formule van Haussdorf is voor de Koch-kromme de dimensie te berekenen. Dat is in dit geval 1,2619.
Een rechte lijn heeft dimensie 1 en het platte vlak heeft dimensie 2.
Een dimensie van 1,2619 betekent zoiets als: geen rechte lijn meer, maar het platte vlak wordt nog lang niet gevuld.
Volgorde van stappen
Wat we in eerste plaatjes hierboven doen, is telkens stap 1 toepassen op elke lijnstukje. Dat wordt hieronder nog eens geïllustreerd met de blauwe lijn (stap 3) waarop we stap 1 toepassen om stap 4 te krijgen.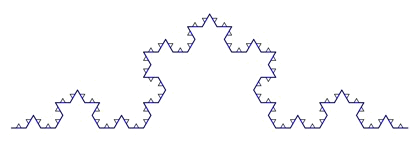
Om stap 4 te krijgen kunnen we ook stap 2 toepassen op stap 2 (blauw), of stap 3 toepassen op stap 1 (blauw):
Dat laatste kunnen we ook benadrukken door middel van kleur in een dynamisch plaatje. Daarmee zien we de hele opbouw van de fractal in één plaatje:
Naar varianten van de Koch-kromme