In de volgende voorbeelden variëren we de lengte van de vier lijnstukken in stap 1. Stap 0 laten we weg, want dat is telkens een lijnstuk met lengte 1.
Lengte = 0,26
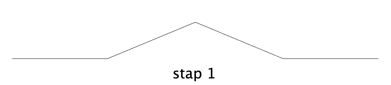
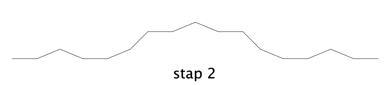
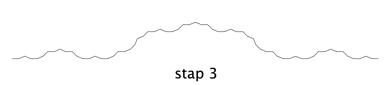
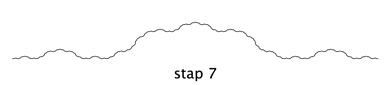
De dimensie is 1,029; nét boven 1, dus vrijwel een rechte lijn. Verder is deze fractal weinig interessant.
Lengte = 0,4
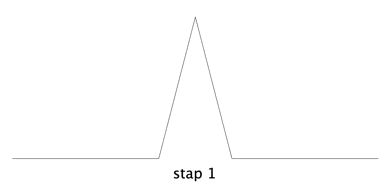



De dimensie is 1,5129; het platte vlak wordt al beter gevuld.
Lengte = 0,48

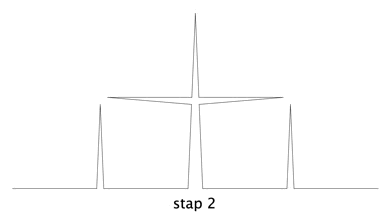
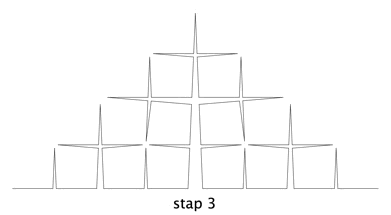

De dimensie is 1,8888; het platte vlak wordt bijna geheel gevuld.
Interessant is het om te zien dat op alle drie zijden van de driehoek dezelfde patronen ontstaan, die elkaar niet raken.
Lengte = 0,5
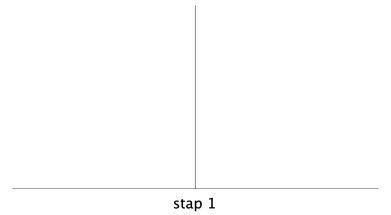

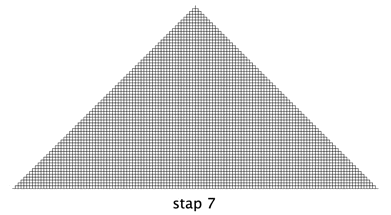
De dimensie is 2; het platte vlak wordt helemaal gevuld.
