Peaks fractals
Als je niet goed weet wat fractals zijn en hoe die werken, bekijk dan eerst even de Introductie van fractals.
Twin Peaks
Hier zie je stap 1 tot en met stap 6 van de Twin Peaks:
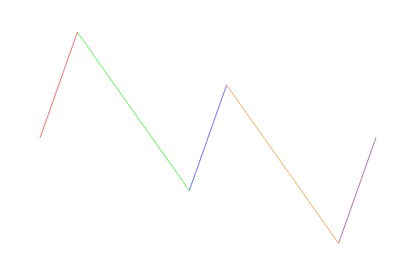
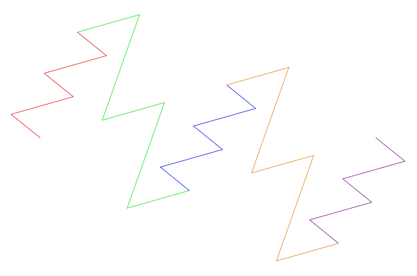




Bovenaan in stap 3 ontstaat een gesloten figuur, die me doet denken aan twee bergtoppen en links een naaldboom; vandaar de naam Twin Peaks.
Dit is een wezenlijk andere fractal dan de Eend-kromme en de Titanic fractals. De verhouding tussen de lengtes van de lange en korte lijnstukken is hier √3. De contouren worden weer heel anders dan bij de Eend-kromme en de Titanic fractals.
Twin Peaks variant
Er is een variant van de Twin Peaks fractal te maken, door in stap 1 de twee langste lijnstukken te vervangen door stap 1.
Hier zie je stap 1 tot en met stap 4 van de Twin Peaks variant:




De contouren van deze fractal zijn gelijk aan die van de Twin Peaks fractal.
Triplet Peaks
Hier zie je stap 1 tot en met stap 4 van de Triple Peaks:




Bovenaan in stap 3 ontstaat een gesloten figuur, die me –een kwart slag gedraaid– doet denken aan drie bergtoppen en links een naaldboom; vandaar de naam Triplet Peaks.
Dit is een wezenlijk andere fractal dan de Eend-kromme, de Titanic fractals en de Twin Peaks. De verhouding tussen de lengtes van de lange en korte lijnstukken is hier √4 = 2.
Quads Peaks
Hier zie je stap 1 tot en met stap 4 van de Quads Peaks:


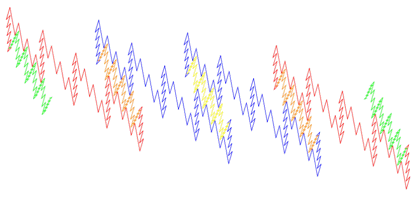
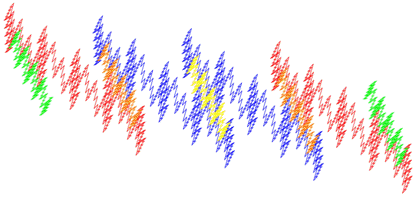
Bovenaan in stap 3 ontstaat een gesloten figuur, die me –een kwart slag gedraaid– doet denken aan vier bergtoppen en links een naaldboom; vandaar de naam Quads Peaks.
Dit is een wezenlijk andere fractal dan de Eend-kromme, de Titanic fractals, de Twin Peaks en de Triplet Peaks. De verhouding tussen de lengtes van de lange en korte lijnstukken is hier √5.
Deze reeks stopt hier: een Quints Peaks is niet mogelijk. Dat is ook te zien aan stap 1 van Triplet Peaks en Quads Peaks: ze zien er steeds platter uit. Bij een Quints Peaks zouden er nog weer twee lijnstukken bij komen, die ook een nog grotere verhouding van √6 tussen de lange en korte lijnstukken moet hebben. Dat past eenvoudig niet meer.
De laatste twee Peaks fractals zijn ook al minder interessant om te zien.
Ingesloten figuren
De ingesloten figuren zijn bij de Triplet Peaks en de Quads Peaks fractals lastig te zien. Het is de moeite waard om de ingesloten figuren van de Eend-kromme en van bovenstaande Peaks fractals nader te bekijken.
De ingesloten figuur van de Eend-kromme, de Eend-figuur, kan met een paar lijnen opgedeeld worden. De vier gelijkzijdige en gelijkvormige driehoeken zijn hierbij ook herkenbaar.

De ingesloten figuur van de Twin Peaks fractal kan met vier lijnen opgedeeld worden, waardoor er rechthoekige driehoeken zichtbaar worden. De zijden van de meeste driehoeken hebben een verhouding van 1, √2, √3. De zijden van de twee langere driehoeken hebben een verhouding van 1, √8, 3. De drie driehoeken aan de rechterkant zijn samen gelijkvormig met de drie driehoeken linksboven, maar dan een factor √3 kleiner. Deze twee groepjes worden gekoppeld door twee gelijke driehoeken links onder. De zijden van de gehele figuur verschillen iedere keer een factor √3 van elkaar.

De ingesloten figuur van de Triplet Peaks fractal kan met vier lijnen opgedeeld worden, waardoor er stomphoekige driehoeken zichtbaar worden. De vier driehoeken aan de rechterkant zijn samen gelijkvormig met de vier driehoeken linksboven, maar dan een factor 2 kleiner. Deze twee groepjes worden gekoppeld door twee gelijke driehoeken links onder. De zijden van de gehele figuur verschillen iedere keer een factor 2 van elkaar.

De ingesloten figuur van de Quads Peaks fractal kan met vier lijnen opgedeeld worden, waardoor er stomphoekige driehoeken zichtbaar worden. De vijf driehoeken aan de rechterkant zijn samen gelijkvormig met de vijf driehoeken linksboven, maar dan een factor √5 kleiner. Deze twee groepjes worden gekoppeld door twee gelijke driehoeken links onder. De zijden van de gehele figuur verschillen iedere keer een factor √5 van elkaar.

Met bovenstaande ingesloten figuren zijn vlakvullingen te maken. Hieronder twee voorbeelden, met de ingesloten figuren van de Eend-kromme en van de Twin Peaks fractal, beide met drie verschillende formaten.


