Animaties met de Eend-kromme
Er zijn mooie animaties te maken met de Eend-kromme en de bekende Terdagon, die je hieronder ziet.
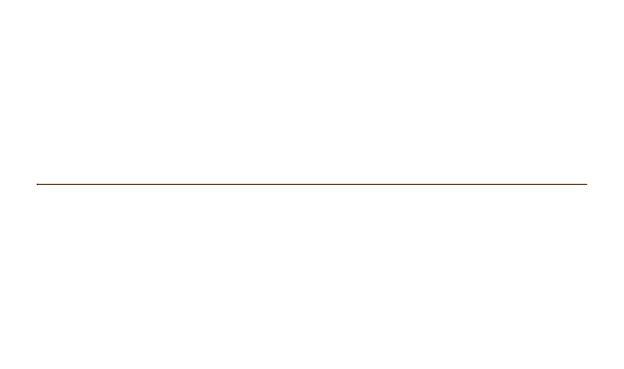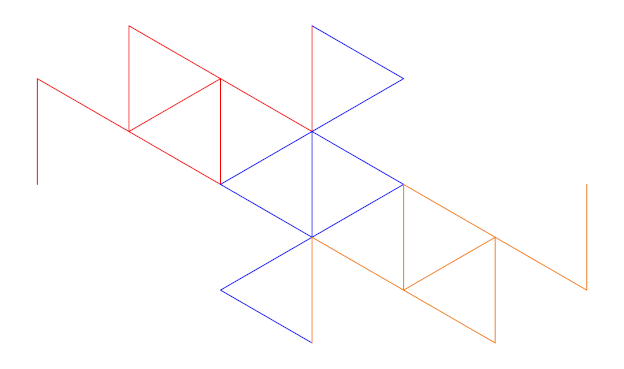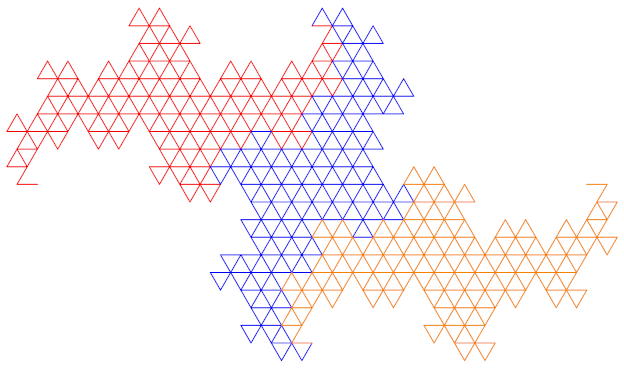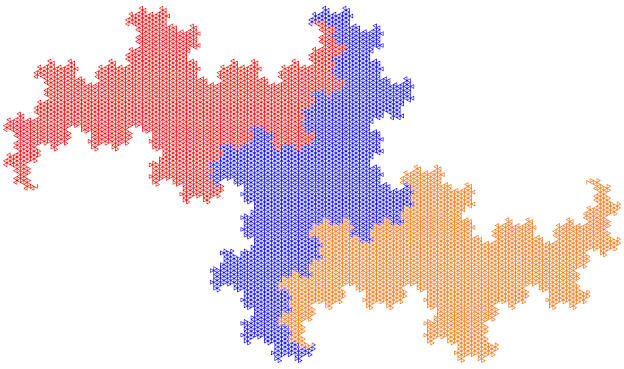
Net als bij de Eend-kromme heeft de Terdragon in stap 1 drie lijnstukken. Bij de Terdragon zijn deze alledrie even lang en ze staan onder een hoek van 60º. Dat maakt dat er gelijkzijdige driehoeken ontstaan.
Bij zowel de Eend-kromme als bij de Terdragon is de dimensie 2 en beide krommen raken elkaar alleen in de hoekpunten. Er zijn geen overlappende of snijdende lijnstukken.
Animaties
Hieronder zie je hoe stap 4 van de Terdragon overgaat in stap 4 van de Eend-kromme. Deze overgang bestaat uit allemaal andere fractals met drie lijnstukken, die steeds ook dimensie 2 hebben. Alleen zijn er nu wel elkaar snijdende lijnstukken. Je ziet hier 81 lijnstukjes bewegen.
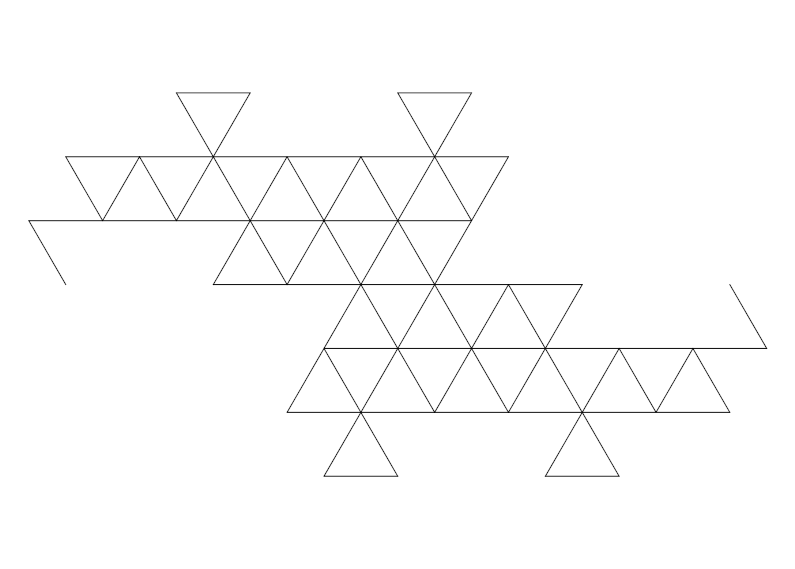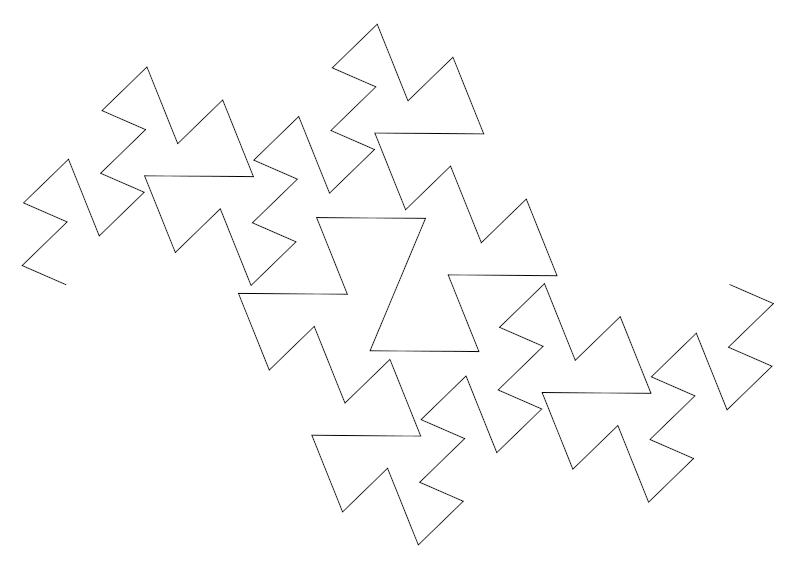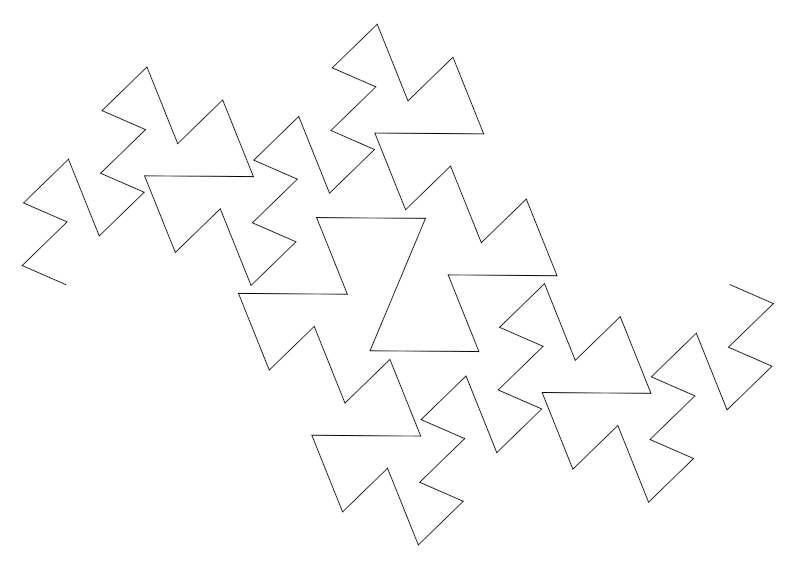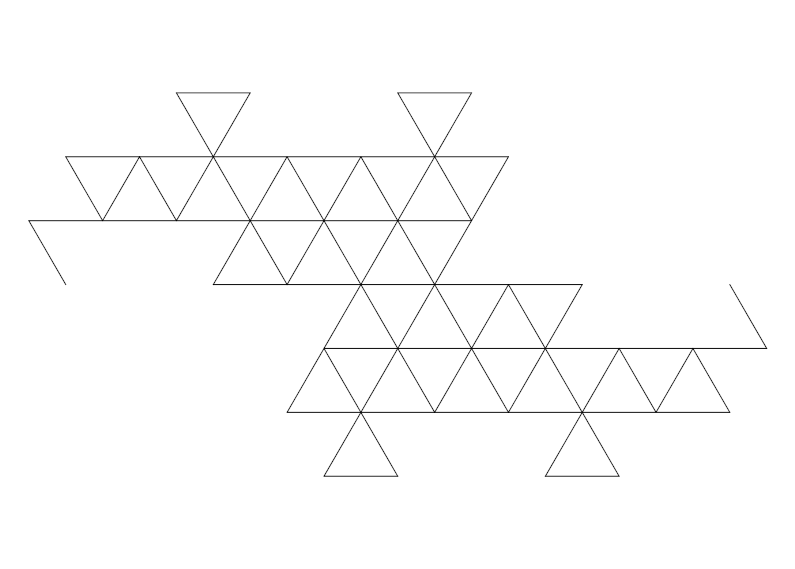
Van stap 6 van de Terdragon naar stap 6 van de Eend-kromme, met 729 lijnstukjes:

Er lijken gaten te ontstaan in de tussenliggende fractals.
Van stap 8 van de Terdragon naar stap 8 van de Eend-kromme, met 6561 lijnstukjes:

De gebieden met elkaar snijdende lijnstukken zien er donkerder uit dan andere gebieden.
Van stap 10 van de Terdragon naar stap 10 van de Eend-kromme, met 59049 lijnstukjes:

De gaten en de donkere gebieden lijken even groot te zijn.
